Generative Models: Flow Matching
Flow matching grew out of two earlier ideas. Normalizing flows showed how to gradually transform simple noise into complex data, while optimal transport studied how to move one distribution into another along efficient paths. Flow matching takes inspiration from both: it learns smooth velocity fields that carry noise toward data without the heavy math of exact Jacobians or transport costs. This simplicity and flexibility helped it quickly gain attention as an alternative to diffusion models. Let's see what it's all about.
Flow matching is a generative paradigm. The goal is to learn a target distribution \(q\) within \(\mathbb{R}^d\) and be able to sample from it. To do so, our approach will be to sample initial points from a source distribution \(p\) and evolve them according to a velocity field that pushes from the high-density areas of \(p\) to the high-density areas of \(q\). Thus, we think in terms of how points, or synonymously particles, from \(p\) are gradually moved through space to become points from \(q\). The time interval will be \([0, 1]\). At \(t=0\) we have \(X_0 \sim p\) and at \(t=1\) we want to have \(X_1 \sim q\).
То move samples from \(p\) to \(q\) we need a velocity field \(u: [0, 1] \times \mathbb{R}^d \rightarrow \mathbb{R}^d\), which outputs the velocity at a given point \(x\) and time \(t\). Of course, the velocity is the derivative of some path \(\psi: [0, 1] \times \mathbb{R}^d \rightarrow \mathbb{R}^d\), which in this case is called a flow. It's defined implicitly using the ODE
Here for simplicity \(\psi_t(x) := \psi(x, t)\) and \(\psi_0(x) = x\). Importantly the flow \(\psi_t(x)\) represents the position at time \(t\) of a particle that has started at \(x\) at \(t=0\). In total, \(\psi(x, \cdot)\) contains the full path of a particle that has started at position \(x\). To compute it, we need to solve the ODE, in practice by numerically integrating the velocity up to some time limit. However, consider that the starting particles have a distribution and naturally, it gets warped in time by the flow. So the flow induces a distribution at any given time, \(p_t\). Technically, \(p_t\) is called the pushforward of the source distribution \(p\) under \(\psi_t\), \(p_t = (\psi_t)_{\#p}\). To sample from an intermediate distribution \(p_t\) we need to sample a particle from \(p\) at \(t=0\) and solve the ODE up to \(t\). The goal of flow matching is to learn a velocity field \(u_t^\theta (x)\) such that its flow generates a distribution path \(p_t\) with \(p_0 = p\) and \(p_1 = q\). In that sense, we'll sample from \(p\) and integrate the velocity to obtain samples from \(q\).
Of course, we'll choose the source distribution to be Gaussian, \(p := p_0 = N(0, I)\). To obtain a distribution path \(p_t\), consider the simplest case, where we sample \(X_0 \sim p\) and \(X_1 \sim q\) from the training dataset, sample a time \(t \sim U[0, 1]\), and define the random variable \(X_t\) to interpolate between \(X_0\) and \(X_1\), that is, \(X_t = tX_1 + (1 - t)X_0 \sim p_t\). What is the distribution of \(X_t\)? In general, it's some complicated one, we don't know. Instead, we'll condition on one particular observation of \(X_1\), say \(X_1 = x_1\). We get
This is a much more tractable distribution. Next, if we differentiate it with respect to time, we derive the target conditional velocity, \(u_t(X_t|X_1, X_0) = X_1 - X_0\), which becomes the target to the learnable predictor \(u_t^\theta(\cdot)\). We thus formulate the conditional flow matching (CFM) loss:
With this simple loss we can learn an accurate velocity field \(u_t^\theta(\cdot)\) that moves points from \(p\) to \(q\). By solving the ODE \(dX_t/dt = u_t^\theta(X_t)\) one can get the pathline of a point. We can recover the ending position by integrating the velocity \(X_0 + \int_{0}^1 u_t^\theta( X_t) dt\) and similarly the distance traveled is given by \(\int_0^1 | u_t^\theta(X_t) | dt\). Importantly, at test time once the sample \(X_0\) is selected, the transformation to \(X_1\) is a deterministic process, unlike, for example, diffusion models.
Consider intuitively how flow matching learns multimodal distributions, shown in Fig. 1. There, we have the source distribution at the bottom and a target bimodal distribution at the top. We sample random pairs \((X_0, X_1)\) along with \(t \sim U[0, 1]\) and compute \(X_t = tX_1 + (1 - t)X_0\). Each point \(X_t\) lies somewhere on the line connecting the sampled \(X_0\) and \(X_1\). The model is supervised to predict the direction toward the target \(X_1\). Note how when \(t \approx 0.5\), the points \(X_t\) fall somewhere inbetween the source and target distributions. There, the flow learns to push them to one of the two target modes. On the contrary, if \(t \approx 0\), then \(X_t \approx X_0\). If we sample such a point \(X_0\) twice and pair it with targets from different modes, the learned velocity will point in the average direction. Thus, at test time, after we sample \(X_0\) the velocity initially pushes it only up. As soon as it starts leaving the high-density regions of the source distribution, it gets randomly picked up by one of the velocities pushing towards the individual modes.

It's not possible to determine which region of the source will be mapped to which region of the target distribution. The model is only trained to approximate the expected velocity field. It never records one-to-one correspondences between base and data samples. Note that because we're training with random \((X_0, X_1, t)\) tuples, during test-time the integration of the velocity field can result in quite nonlinear motion. It is generally not the case that points from one region will move with constant velocity in a straight path to some target region. To see this, consider the animation in Fig. 2. There, the noisy particles sampled at the beginning are all first contracted and pushed toward the center, so that the range of values matches the range of the targets. After around \(t\approx 0.4\), the velocity in the center increases in magnitude and starts pushing outward, while the velocity outside the circle still pushes inward. These forces eventually form the target distribution's circular shape.
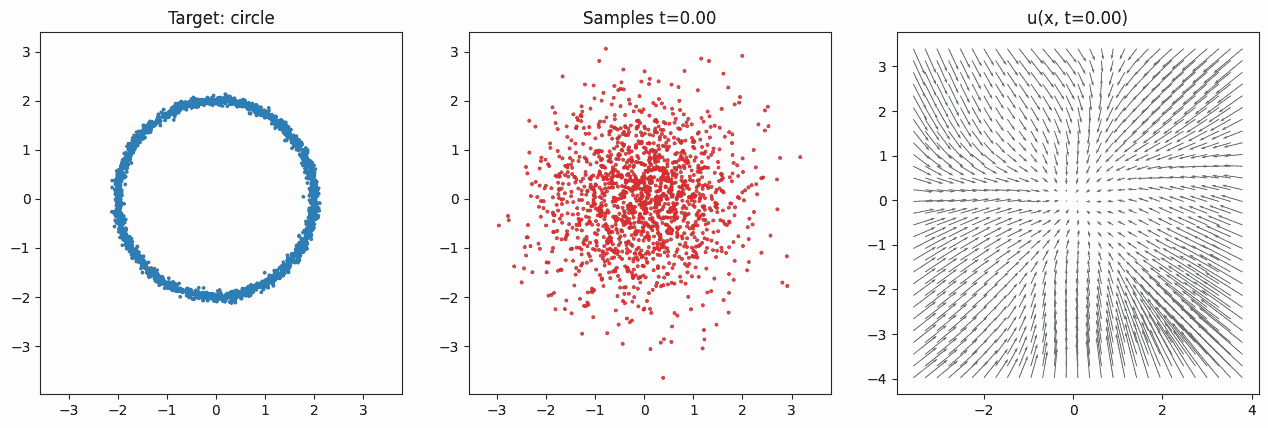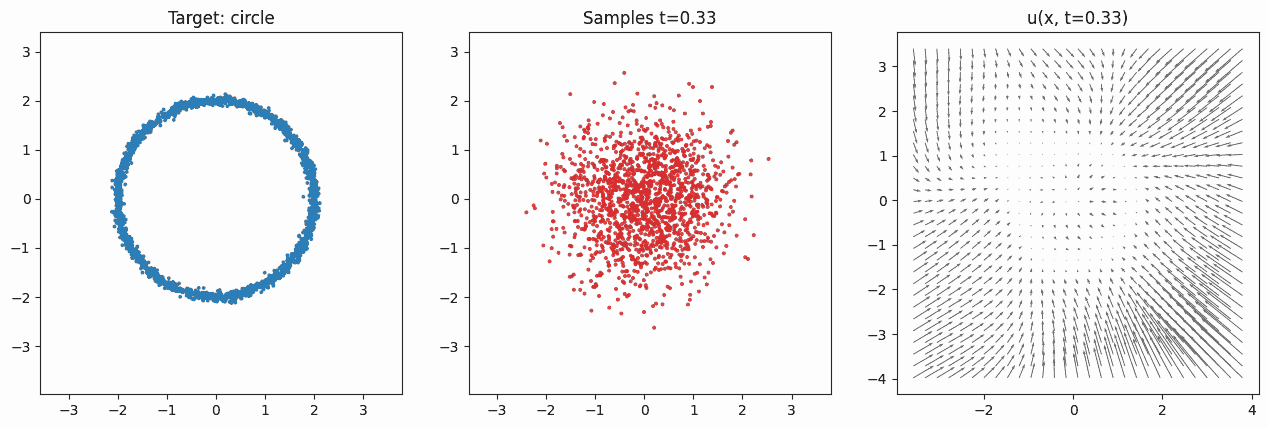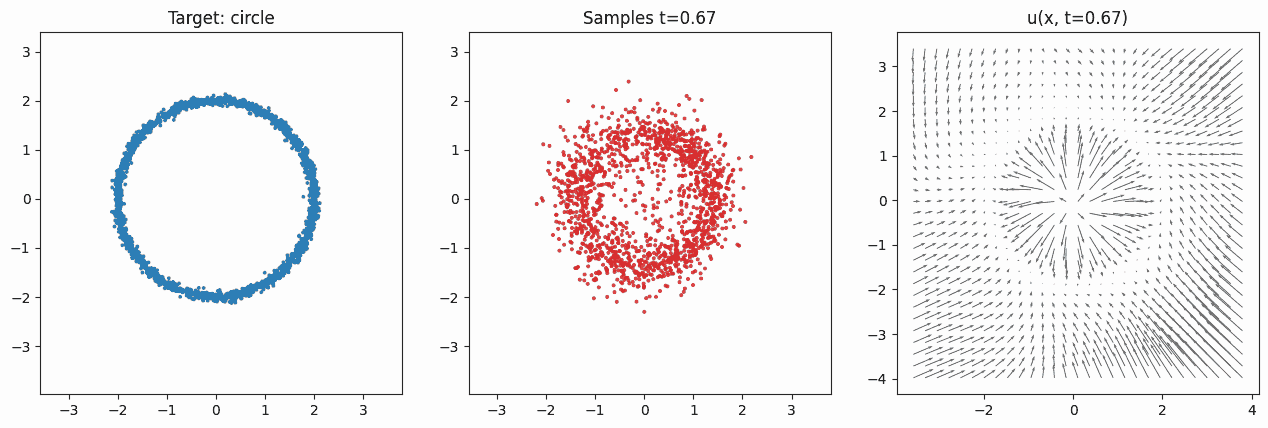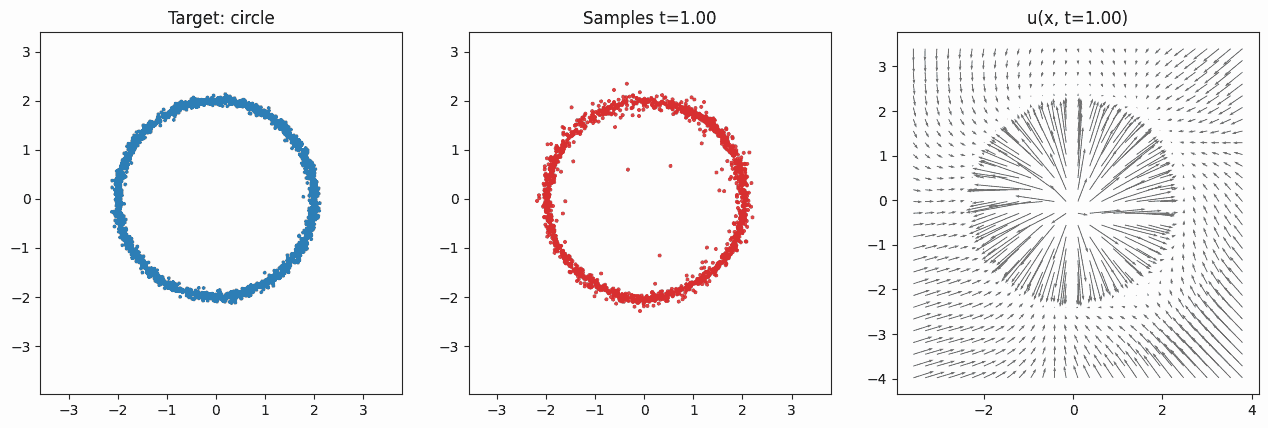
That is the basic idea of flow matching. Beyond it, there are many generalizations and domain-specific adaptations [1]. For example, one can do flow matching on general Riemannian manifolds. The above examples are in Euclidean space, which is flat and has zero curvature. Instead, a Riemannian manifold is a space which is locally Euclidean (the neighborhood of each point can be thought as having Euclidean-like properties) and for each point we can define a smoothly-varying inner product between elements in the tangent space at that point.
In the simplest terms, Riemannian manifolds include spherical, hyperbolic, toroidal, and all kinds of other geometries. If we want to model the weather distribution on the Earth's surface, one will likely have to use flow matching on a sphere. Similarly, to learn distributions over camera poses in computer vision or to predict protein structure in 3D we need to do flow matching in the \(SE(3)\) group. \(SE(3)\), the special Euclidean group in three dimensions, represents all possible rigid-body motions (or equivalently poses) in 3D. Intuitively, if we fix a particular pose \((\mathbf{R}, \mathbf{t})\) then its tangent space is locally Euclidean and consists of all nearby infinitesimal motions - angular velocities \(\omega \in \mathbb{R}^3\) and linear velocities \(v \in \mathbb{R}^3\). If \((\omega_1, v_1)\) and \((\omega_2, v_2)\) are two infinitesimal twists (motions), with a well-defined inner product we can compute an "angle" between them, \(\cos \theta = \big\langle (\omega_1, v_1), (\omega_2, v_2) \big\rangle / \big( \lVert (\omega_1, v_1) \rVert \lVert (\omega_2, v_2) \rVert \big)\). And that's how we can define "angles" between pose transformations. For such spaces flow matching needs appropriate adaptations.
Relations with diffusion. Both diffusion and flow matching introduce intermediate distributions, \(q(x_t |x_0)\) and \(p_t\), respectively. Diffusion does this with a noisy stochastic process, while flow matching uses a deterministic ODE. Both require test-time compute: diffusion integrates a denoising process (often with Langevin dynamics), and flow matching integrates a velocity field. On a technical level, the forward SDEs used in diffusion with affine drift produce Gaussian conditional distributions \(q(x_t | x_0)\). Flow matching often defines its reference distribution paths in exactly this Gaussian form.
Applications
Robotic actions. Now, let's see some exciting applications of flow matching. In robotics flow matching is used in the famous Pi-Zero model [2], which is supposed to be a generalist vision-language-action (VLA) model. A foundational model for robots is the holy grail of robotics, with its goal of being able to accurately execute any task in the physical world. If you tell it to "clean up the house" it will use its language module to understand the task, its vision module to make sense of its surroundings, its action module to predict the right actions, and its embodiment to execute them. Embodiment here refers to the physical aspects of the robot - whether it has a gripper, wheels, arms, how many joints, what do actions represent and so on.
The Pi-Zero architecture extends a VLM with an action expert. The task is formulated as learning a data distribution over actions given observations \(p(\mathbf{A}_t | \mathbf{o}_t)\) where actions are actually action chunks of length \(H\), \(\mathbf{A}_t = [\mathbf{a}_t, \mathbf{a}_{t+1}, ..., \mathbf{a}_{t+H-1}]\), and observations contain images, user prompts and the current robot state, \(\mathbf{o}_t = [\mathbf{I}_t^1, ..., \mathbf{I}_t^n, \ell_t, \mathbf{q}_t]\). Here there are \(n\) images, \(\mathbf{I}_t^n\), in the current timestep \(t\), \(\ell_t\) is a sequence of language tokens for the task, and \(\mathbf{q}_t\) is a vector of joint angles representing the robot's proprioception. For cross-embodiment training we pad the vector of the robot's state with zeros, up to some limit. To predict continuous actions, each action in the action chunk has its own token from which the continuous value is decoded. The training loss is:
where \(t\) is the frame timestep, \(\tau\) is the flow matching timestep, and for the distribution path the authors use linear interpolation, \(q(\mathbf{A}_t^\tau | \mathbf{A}_t) = N(\tau \mathbf{A}_t, (1 - \tau)\mathbf{I})\). Thus, quite similar to what we saw above. The next version of the model, called Pi-0.5 [3] retains the flow matching.
Policy Gradients. Another interesting application is Flow Policy Optimization (FPO) [4]. It's an alternative to the good-old PPO [5]. The goal of FPO is to redirect the policy's action probability to high return behavior. Compared to parametrizing the policy as a Gaussian with predicted mean and standard deviation, a flow model for the actions is much more expressive. During rollouts one needs to integrate the velocity field for a few steps to get an action. During training the only thing we'll change in PPO is the likelihood ratio \(r(\theta) = \pi_\theta(a_t | o_t) / \pi_{\theta_\text{old}}(a_t | o_t)\). If we fix an action-observation pair \((a_t, o_t)\) we can compute the conditional flow matching loss that represents how well the policy predicts the velocity toward \(a_t - \epsilon\) (some noisy sample) with both the initial policy weights \(\theta_\text{old}\) and the current ones, \(\theta\), after a few updates. Thus, the ratio becomes
So basically, you take your stored \((a_t, o_t, r_t)\), estimate advantage \(A_t\), compute the loss measuring how well the policy network estimates the velocity from a perturbed \(a_t^\tau\) toward \(a_t\), compute the exponentiated loss difference \(r(\theta)\), weight by advantages, and backprop. The gradient goes through the term \(r(\theta)\) and reaches the policy, changing the modeled velocity toward actions with higher \(A_t\).
Overall, flow matching has established itself as a versatile technique for multimodal complex data generation. Ongoing work explores conditional guidance, faster solvers, techniques to incorporate hard constraints, and extensions to discrete domains. Exciting :)
References
[1] Lipman, Yaron, et al. Flow matching guide and code. arXiv preprint arXiv:2412.06264 (2024).
[2] Black, Kevin, et al. π0: A vision-language-action flow model for general robot control. arXiv, preprint arXiv:2410.24164 (2024).
[3] Black, Kevin, et al. π0.5: a Vision-Language-Action Model with Open-World Generalization. arXiv, preprint arXiv:2504.16054 (2025).
[4] McAllister, David, et al. Flow Matching Policy Gradients. arXiv preprint arXiv:2507.21053 (2025).
[5] Schulman, John, et al. Proximal policy optimization algorithms. arXiv:1707.06347 (2017).