Infinitely Wide Neural Networks | The Critical Section

Deep neural networks seem to break the common U-shaped bias-variance risk curve. Current state-of-the-art networks have significantly more parameters than dataset samples, and yet still perform surprisingly well on the test set. We can't really say they're overfitting. So what's going on? This post explores recent results and insights around over-parameterized networks and their supposedly different training regimes. In particular, a lot of intuition can be gained from analyzing what happens in networks with infinitely many units in the hidden layers.

Bayesian Inference

The first major limiting result is that infinitely wide neural networks are Gaussian processes. A Gaussian process is a stochastic process such that any finite collection of random variables from it, have a joint Gaussian distribution. Intuitively, we can think of it like a probability distribution on functions $f(x)$, such that if one selects a number of points $\{x_1, ..., x_N\}$, then the corresponding sampled values $\{f(x_1), ..., f(x_N)\}$ come from a multidimensional normal distribution with mean vector $\{m(x_1), ..., m(x_N) \}$ and a $N \times N$ covariance matrix $\Sigma$ containing the covariances between $f(x_i)$ and $f(x_j)$, for $1 \le i, j \le N$.

In practice, instead of specifying the covariance matrix for any finite set of variables, we use a kernel function $k(\cdot, \cdot)$ which takes in a pair of elements $x$ and $x'$ and computes their covariance $k(x, x')$:

$$ \begin{align} f(x) \sim GP(m(x), k(\cdot, \cdot)) \Leftrightarrow & \\ {\small \begin{bmatrix} f(x_1) \\ \vdots \\ f(x_N) \\ \end{bmatrix} } \sim & \ \mathcal{N} \Big( \mu = {\small \begin{bmatrix} m(x_1) \\ \vdots \\ m(x_2) \\ \end{bmatrix}}, \Sigma = {\small \begin{bmatrix} k(x_1, x_1) & \cdots & k(x_1, x_N) \\ \vdots & \ddots & \vdots \\ k(x_N, x_1) & \cdots & k(x_N, x_N) \\ \end{bmatrix}} \Big ) \end{align}$$

A Gaussian process is completely specified by its mean function $m(x)$ and its kernel function $k(\cdot, \cdot)$. Hence, to describe the GP generated by a infinitely wide neural network we'll have to specify its mean and kernel.

Suppose we have a network with $L$ layers and the number of units in layer $l$ is $n^l$. We'll annotate the pre-activations as $\textbf{z}^l$ and the post-activations (after applying a nonlinearity) with $\textbf{y}^l$, with the convention that the input is $\textbf{x} = \textbf{y}^0$. The first hidden layer is $\textbf{z}^0$. After we apply the element-wise activation $\phi(\cdot)$, we get $\textbf{y}^{l + 1} = \phi(\textbf{z}^l)$. The weights for layer $l$ are initialized randomly from $\mathcal{N}(0, \frac{\sigma^2_w}{n^l})$ and those for the biases from $\mathcal{N}(0, \sigma^2_b)$.

The random initialization of the parameters of the network induces a probability distribution on its outputs. Sampling different parameters will produce different outputs for the same inputs. Likewise, we can talk about the function being modelled as also coming from a probability distribution over functions. This distribution is hard to characterize. However, the main point is that in a network with infinitely many hidden units, this distribution over functions becomes a Gaussian process. Let's see how this happens.

Considering layer $l$ we note that its weights $\textbf{W}^l$ and biases $\textbf{b}^l$ are random Gaussian variables. If we condition on the previous activations $\textbf{y}^l$, then the pre-activations $\textbf{z}^l$ are just a linear map of the independent Gaussian random variables from the weights and the biases. As a result, the pre-activations are also independent and Gaussian. This is true even with finitely wide layers.

$$ \textbf{z}^l|\textbf{y}^l \sim GP(\textbf{0}, \sigma^2_2 K^l + \sigma^2_b) $$

$K^l$ is the second moment matrix of previous activations and $K^l(\textbf{x}, \textbf{x}') = \frac{1}{n^l}\sum_{i = 1}^{n^l} y_i(\textbf{x}) y_i(\textbf{x}')$.
What does it mean that $\textbf{z}^l | \textbf{y}^l$ is a Gaussian process? It means that if we pick two inputs $\textbf{x}$ and $\textbf{x}'$, and we propagate them up to layer $l$, then we'll get $\textbf{y}^l(x)$ and $\textbf{y}^l(x')$. These two values will have a covariance given by $K^l(\textbf{x}, \textbf{x}')$. Conditioning on $\textbf{y}^l(\textbf{x})$ and $\textbf{y}^l(\textbf{x}')$, we can sample various weights for $\textbf{W}^l$ and $\textbf{b}^l$, and the distribution on the resulting function $\textbf{z}^l$ will be a Gaussian process.

We can also say that $\textbf{z}^l$ depends on $K^l$, so technically $\textbf{z}^l \| K^l$ is a Gaussian process with zero mean and the same kernel. Now, we condition $K^l$ on the previous pre-activations $\textbf{z}^{l-1}$:

$$ K^l(\textbf{x}, \textbf{x}') = \frac{1}{n^l} \sum_{i = 1}^{n^l} y^l_i(\textbf{x}) y^l_i(\textbf{x}') = \frac{1}{n^l} \sum_{i = 1}^{n^l} \phi(z_i^{l-1}(\textbf{x})) \phi(z_i^{l-1}(\textbf{x}')) $$

Since $\textbf{z}^{l - 1} \| K^{l - 1}$ is a GP, then $K^l(\textbf{x}, \textbf{x}')$ is calculated by sampling $n^l$ pairs of points $z_i^{l-1}(\textbf{x})$ and $z_i^{l-1}(\textbf{x}')$, applying $\phi(\cdot)$, multiplying them, and averaging. And here's the crucial part. If $n^l \rightarrow \infty$, then the result of this averaging becomes deterministic (as we are averaging over infinitely many samples), and $K^l(\textbf{x}, \textbf{x}') = \mathbb{E}[\phi(\textbf{z}^{l-1}(\textbf{x})) \phi(\textbf{z}^{l-1}(\textbf{x}'))]$. Even better, this can be calculated analytically for some specific activations like $\text{ReLU}$, $\text{GeLU}$, and $\text{erf}$. Thus $K^l \| K^{l-1}$ becomes deterministic as $n^l \rightarrow \infty$.

At this point, if all layer widths go to infinity, we can recursively define $K^l$ as an exact deterministic calculation of $K^0$ assuming we can solve the expectation integrals above. $K^0(\textbf{x}, \textbf{x}')$ is simply $\frac{1}{n^0} \sum_{i = 1}^{n^0} x_i x'_i$ and based on it, we can compute the kernel function of the network output. The Gaussian process resulting from the last layer of an infinite width neural network is called the Neural Network Gaussian Process (NNGP). It's zero centered, and its kernel function is defined recursively, as described above.

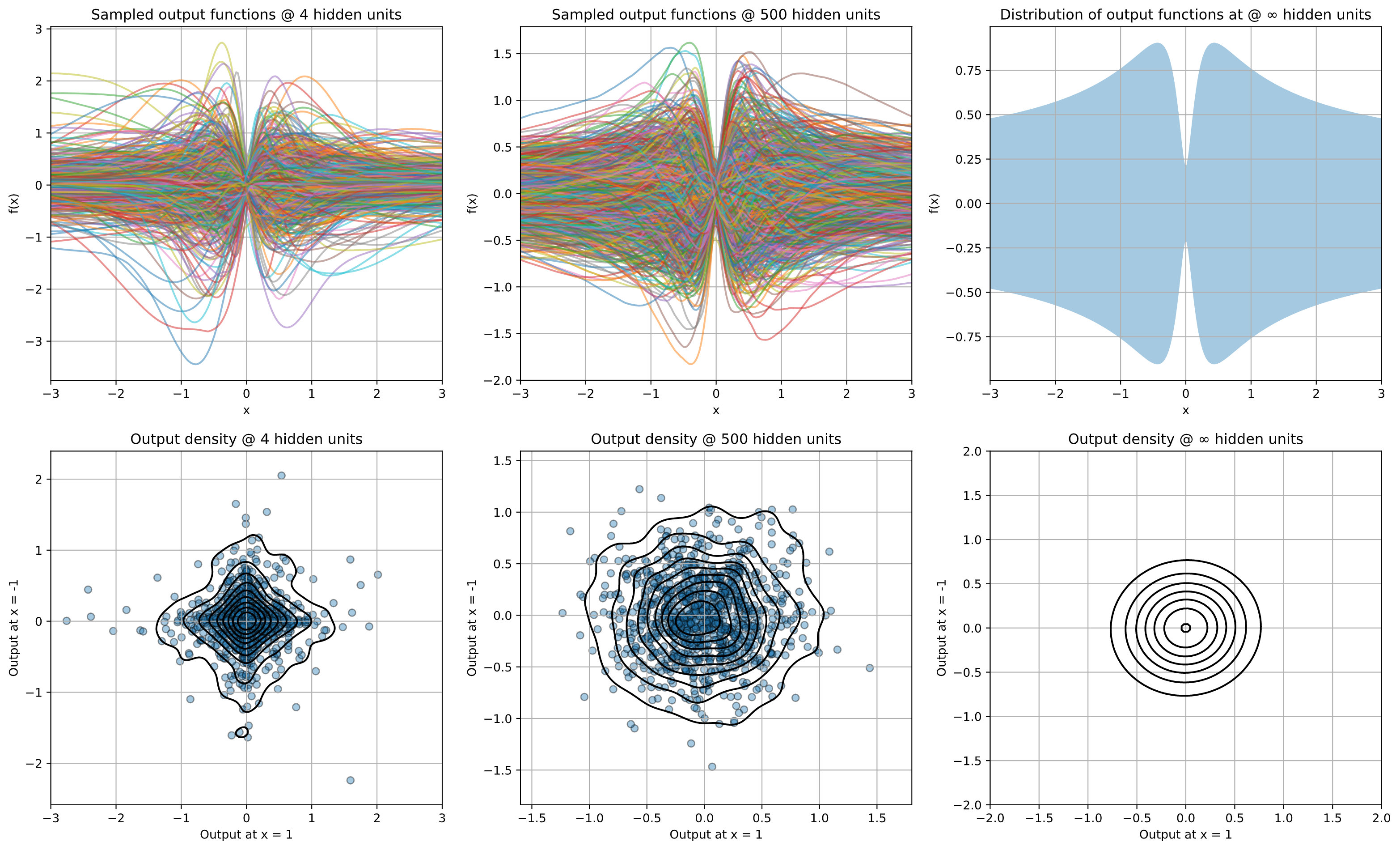
Figure 1 shows how for a fixed architecture, adding more hidden units makes the finite outputs more Gaussian-like. The random weights induce a distribution on output functions. By sampling different sets of weights, we can sample the corresponding output functions. Likewise, we can look at the distribution of outputs for specific fixed inputs. As the hidden layers become wider, this distribution converges to a Gaussian.

Figure 1: The Gabor-Relu NNGP. We investigate a 3-layer network. All layers are linear. After the first layer we apply a Gabor activation and after the second one - a ReLU activation. The input data is one dimensional. The columns show how 4, 500, and infinite hidden units in the first two layers affect the predictions. The rows show various sampled functions and their outputs for two fixed inputs.

Most reasonable network architectures define a NNGP with its own kernel and once we have the kernel, we can do predictions. Let $\textbf{X}$ be the training set, $\textbf{X}_*$ the test set, $\textbf{Y}$ the training labels, and $k(\cdot, \cdot)$ the kernel function. The standard posterior predictive distribution from a GP is given by

$$ \textbf{Y}_* | \textbf{X}, \textbf{X}_*, \textbf{Y} \sim \mathcal{N} \Big(k(\textbf{X}_*, \textbf{X})k(\textbf{X}, \textbf{X})^{-1}\textbf{Y}, \Sigma \Big)\\ \text{where } \Sigma = k(\textbf{X}_*, \textbf{X}_*) - k(\textbf{X}_*, \textbf{X})k(\textbf{X}, \textbf{X})^{-1}k(\textbf{X}, \textbf{X}_*). $$

Prediction from the NNGP in this way corresponds to exact Bayesian inference. However, this is not the only interpretation. It can be proven that an infinitely wide network trained with gradient descent to minimize the MSE loss but with all layers except the last one frozen (fixed at initialization), converges to a function sampled from the NNGP posterior [1]. To rephrase, if we train only the last layer of the network infinitely long, then the distribution of its output functions will converge to the exact corresponding NNGP.

What happens if we train all layers, not only the last one? There are exciting recent results answering this question.

Gradient Descent

Let's set some notation. Let $f(\cdot, \theta)$ represent a neural network with parameters $\theta$, flattened across all layers. We have a standard supervised seeting where the output on training sample $\textbf{x}$ is $f(\textbf{x}, \theta)$, the corresponding label is $y$, and the loss on that sample is $\ell(f(\textbf{x}, \theta), y)$, which could be the mean squared loss, binary cross entropy loss, or any other loss function. The training set contains $N$ samples, $\textbf{X} = \{\textbf{x}_1, \textbf{x}_2, ..., \textbf{x}_N \}$, along with their corresponding labels $Y = \{y_1, y_2, ..., y_N \}$.

The loss that we are minimizing is averaged across all samples in the training set:

$$ J = \frac{1}{N} \sum_{i = 1}^N \ell(f(\textbf{x}_i, \theta), y_i). $$

With gradient descent we minimize $J$ by repeatedly computing the gradient $\nabla_\theta J$ and taking a small step $\eta$ in the opposite direction from it. The gradient of the loss function with respect to the parameters is given by

$$ \nabla_\theta J = \frac{1}{N} \sum_{i = 1}^N \nabla_\theta f(\textbf{x}_i, \theta) \nabla_f \ell(f(\textbf{x}_i, \theta), y_i). $$

If the step size $\eta$ is infinitesimally small, we can actually model the change in the weights $\theta$ through time as a derivative, instead of a sequence of discrete updates:

$$ \frac{d\theta}{dt} = - \frac{1}{N} \sum_{i = 1}^N \nabla_\theta f(\textbf{x}_i, \theta) \nabla_f \ell(f(\textbf{x}_i, \theta), y_i). $$

This is called continuous gradient descent, or even gradient flow. It simply shows that if the learning rate is very small and we let the neural network train for a very long time, the instantaneous change in the parameters depends on the gradient of the loss function at the current parameters, averaged across the training samples. This is how the network evolves in parameter space. But we can also look at how it evolves in function space.

Let's fix a single sample $\textbf{x}$ and look at how the network output for $\textbf{x}$ changes with time. That is, we want to calculate $\frac{df(\textbf{x}, \theta)}{dt}$. This derivative is given by the chain rule.

$$ \frac{df(\textbf{x}, \theta)}{dt} = \frac{df(\textbf{x}, \theta)}{d\theta} \frac{d\theta}{dt} = - \frac{1}{N} \sum_{i = 1}^N \nabla_\theta f(\textbf{x}, \theta)^T \nabla_\theta f(\textbf{x}_i, \theta) \nabla_f \ell(f(\textbf{x}_i, \theta), y_i). $$

The main quantity of interest here is $\nabla_\theta f(\textbf{x}, \theta)^T \nabla_\theta f(\textbf{x}_i, \theta)$, which is called the neural tangent kernel (NTK) [2]. This is a very important quantity because it directly shows how the network evolves in function space under gradient descent.

Let's write the NTK between two data points $\textbf{x}$ and $\textbf{x}'$ as $\Theta(\textbf{x}, \textbf{x}') = \nabla_\theta f(\textbf{x}, \theta)^T \nabla_\theta f(\textbf{x}', \theta)$. It is the dot product between the gradients of the network output w.r.t. the parameters evaluated at $\textbf{x}$ and $\textbf{x}'$, and is therefore symmetric, as all kernels should be. It depends on $\theta$ and hence, as $\theta$ changes, the NTK changes. Since all the weights and biases $\theta$ are initialized randomly, the NTK is also random.

Similar to the NNGP case, under infinitely wide layers, the NTK also becomes deterministic and constant [2, 3]. Thus, infinitely wide networks have a NTK that does not change with time and is deterministic, completely independent of the weights initialization. Similar to the NNGP kernel, it can be computed recursively. Let's indicate this constant NTK evaluated on the training set with $\Theta(\textbf{X}, \textbf{X}) = \Theta_\infty$. It has the usual kernel matrix shape of $N \times N$ where $N$ is the number of training samples, assuming the network output dimension is 1.

With a deterministic and constant NTK, we can solve for the training dynamics. Let's write the predictions on all training samples $\textbf{X}$ simply as $f(\theta)$. Then, under gradient descent, we have to solve

$$ \frac{df(\theta)}{dt} = -\eta \Theta_\infty \nabla_f \ell(f(\theta), Y). $$

Depending on the loss function, this may not have an analytical solution and we may need to use an ODE solver. However, with a squared error loss $\frac{1}{2}(f(\theta) - Y)^T(f(\theta) - Y)$, things simplify considerably and we can get an exact solution to the training dynamics:

$$ \frac{df(\theta)}{dt} = -\eta \Theta_\infty (f(\theta)- Y) \\ f(\theta) = f(\theta(0)) e^{-\eta \Theta_\infty t} + (I - e^{-\eta \Theta_\infty t}) Y. $$

At $t = 0$, we simply get $f(\theta(0))$. As $t \rightarrow \infty$, an infinite network fits all training samples perfectly, i.e. $f(\theta) \rightarrow Y$. It converges exponentially fast and even allows us to estimate the output function at finite training times by simply plugging in the corresponding $t$.

Apart from the guaranteed convergence to the target labels, infinite networks have other interesting aspects when training with gradient descent. It has been observed empirically that with larger models the final weights after training are not that different compared to the starting weights, and yet the network manages to learn the relationships well. It seems that with many parameters, the output function can change rapidly by changing all the weights only marginally, an effect called lazy training [4].

The fact that weights stay close to their initial values implies that very large and over-parameterized networks are well explained by their first-order approximation around the initial weights.

$$ f(\textbf{x}, \theta(t)) \approx f(\textbf{x}, \theta(0)) + \nabla_\theta f(\textbf{x}, \theta(t))^T (\theta(t) - \theta(0)) $$

In fact, there is a very powerful theorem stating that that under some slight assumptions, the difference between the output of the linearized network and the non-linearized one scales as $O(1/\sqrt{n})$, where $n$ is the number of units in the hidden layers [1]. Same for the difference between the starting and ending parameters, and the difference between the NTK at time $t$ and at time $0$. This proves that large width networks are well-approximated by their linearized versions.

A single network, infinitely wide or not, still models random functions because the initial weights are sampled randomly. The distribution of the weights induces a distribution over networks trained with gradient descent. Luckily, this distribution is known and computable, as long as the width goes to infinity. Specifically, the predictions on a finite set of test points have a multivariate Gaussian distribution, with a specific mean vector and covariance matrix all dependent on the NTK $\Theta_\infty$.

This allows us to talk about the distribution of infinite width networks with a given architecture, trained with gradient descent. To marginalize out the initial weights, one can even predict with an infinite ensemble of such infinite networks. Figure 2 compares the predictions from NNGP and from an infinite ensemble of infinite networks trained with gradient descent infinitely long. Yes, computing this is entirely possible [5, 6].

NNGP, NTK predictions — Figure 2: A comparison of the predictions from NNGP and NTK dynamics on a toy task. The shading shows a 95% confidence interval around the mean predictions. There are 10 training points - considerably fewer than the 100 testing points. As a result, both the Bayesian inference from NNGP and the NTK fail to predict well on the test set. Both predict very well on the training set.

Note that this specific Gaussian distribution (of the outputs of an infinite network trained with gradient descent) does not have a posterior interpretation, like the one from NNGP. Curiously, we can get a posterior interpretation by simply using the NTK $\Theta_\infty$ in the GP predictive formula. This would correspond to training functions of the type $f(\textbf{x}, \theta) + \delta(\textbf{x})$ where $\delta(\cdot)$ is a random untrainable function that just adds a controlled amount of variance [7].

In any case, the two kernels NTK and NNGP offer insights into what happens when the layer widths are infinite and how this affects gradient descent. This is a beautiful little niche area of deep learning which may prove to be quite useful in the upcoming years. I'm looking forward to seeing whether it can be tied to other topics like generalization or optimal architecture search.

References

[1] Lee, J. and Xiao, L. et al. Wide Neural Networks of Any Depth Evolve as Linear Models Under Gradient Descent arXiv preprint arXiv:1902.06720 (2019).
[2] Jacot, A., Gabriel, F., Hongler, C. Neural Tangent Kernel: Convergence and Generalization in Neural Networks arXiv preprint arXiv:1806.07572 (2018).
[3] Arora, S. et al. On Exact Computation with an Infinitely Wide Neural Net arXiv preprint arXiv:1904.11955 (2019).
[4] Chizat, L., Oyalon, E., Bach, F. On Lazy Training in Differentiable Programming arXiv preprint arXiv:1812.07956 (2018).
[5] Novak, R. et al. Neural Tangents: Fast and Easy Infinite Neural Networks in Python arXiv preprint arXiv:1912.02803 (2019).
[6] Novak, R., Sohl-Dickstein, J. and Schoenholz, S. Fast Finite Width Neural Tangent Kernel arXiv preprint arXiv:2206.08720 (2022).
[7] He, B., Lakshminarayanan, B. and Teh, Y. W. Bayesian Deep Ensembles via the Neural Tangent Kernel arXiv preprint arXiv:2007.05864 (2020).
[8] Weng, L. Some math behind neural tangent kernel Lil’Log (Sep 2022).
[9] Understanding the Neural Tangent Kernel Rajat's Blog.