The Ising Model | The Critical Section

The Ising model is a curious little toy model for ferromagnetism in the field of statistical mechanics. While surprisingly simple in terms of definition, it is able to produce very interesting various outcomes, whose explanations are in my opinion, quite deep. This post aims to give a quick introduction to the model, how to sample from it, and how to solve it analytically in one dimension.

Introduction

The Ising model consists of a grid of $n$ sites, where each site $s_i$ can have a positive spin or negative spin, i.e. $s_i \in \{+1, -1\}$. Let's call $n$ the size of the system. Then just based on that, we can say that the system has $N = 2^n$ possible states, where each state consists of the actual spins for all sites.

The energy of each spin depends also on the spins of the neighboring sites and in a $2$-dimensional Ising model these neighbors are the sites to the north, south, east and west. The interaction between two neighboring states $s_i$ and $s_j$ is modeled with the term $-s_i s_j$ which suggests a ferromagnetic relationship where this quantity is $1$ if $s_i$ and $s_j$ have different spins and $-1$ otherwise. The state of the system, consisting of all spins $s_i$, has overall energy $E(s) = -\sum_i \sum_j s_i s_j$. Since physical systems generally try to be in a state that minimizes their energy, we have it that the system will be in a minimum-energy state if the spins at all sites are the same (which is what keeps the system magnetized).

Importantly, the state in which the system will eventually end up may not be the minimum energy one. We model that equilibrium state as a random variable with a Boltzmann distribution:

$$ P_{eq}(s) = \frac{\exp(-\beta E(s))}{\sum_s \exp(-\beta E(s))}. $$

Here $E(s)$ is the energy of the state as defined above and $\beta = \frac{1}{T}$ is a coefficient depending on the temperature $T$. Generally, if $T \rightarrow \infty$, and therefore $\beta \rightarrow 0$, the system is equally likely to be in any of the states. If, on the other hand, $T \rightarrow 0$, and therefore $\beta \rightarrow \infty$, the system has positive probability of being only in states with minimal energy.

Typically, we might be interested in the magnetization, defined as the average spin $m = \frac{1}{n}\sum_i s_i$ over all sites and how it depends on the temperature $T$.

Moving slightly into "physics" territory, we know that of the $N=2^n$ possible states, many will have the same energy. We can group these states into macrostates. The probability that we end up in a given macrostate is, again, given by the Boltzmann distribution and is proportional to $W \mathrm{e}^{-\beta E}$, where $W$ is the number of states in a given macrostate with energy $E$. The log of $W$ is called the entropy, labeled $S$, and since $W = \mathrm{e}^{\ln W}$, we can express $W \mathrm{e}^{-\beta E}$ as $\mathrm{e}^{S - \beta E} = \mathrm{e}^{-\beta (E - TS)}$. The quantity $E - TS$ is the free energy and the most likely state is the one with minimal free energy.

The samples from the equilibrium distribution of the Ising model are very different, depending on the temperature. As it turns out, when $n \rightarrow \infty$, there is a critical temperature $T_c$ above which the system is unmagnetized, and below which it is highly magnetized. At and very close near the critical temperature the system exhibits scale-free behaviour (see figure 1 below).

Above the critical temperature, states tend to become equally likely and the equilibrium distribution becomes uniform as $T \rightarrow \infty$. The spin in site $s_i$ can be "up" or "down" with equal probability, irrespective of the neighboring spins. At finite but large temperatures, the spins are clumped together in very small clusters whose correlation to other clusters falls off rapidly with the distance.

Below the critical temperature all is still in the arctic wilderness. Even the tiniest movement faces an unfathomable amount of resistence. The system is magnetized and most of the spins are either "up" or "down", with only very small clusters scattered throughout. These clusters have finite size and their distribution has an exponential tail. Correlations in the state space are strong and wide.

At the critical temperature $T_c$, the average size of the clumps of correlated spins diverges. The size of each cluster has a power-law distribution and thus much larger, and in some cases even arbitrarily large clusters can appear. They are also scale-free, meaning that if we "zoom out", the resulting distribution will be the same.

Ising samples — Figure 1: Three samples from the Ising model. The left one is a perfect sample from the equilibrium distribution at supercritical temperature. The middle one comes from an approximation to the equlibrium distribution at the critical temperature. The right one is also a sample from an approximated equilibrium, but at subcritical temperature.

Approximate sampling

Sampling from the equilibrium distribution at a certain temperature can be done using a Markov chain with Metropolis dynamics. In principle a simple idea is to select a random site $s_i$ and compute the change in the energy $\Delta E$ that would result if we flip its spin. Then if the flip reduces the energy, we do it. If it increases the energy, we still do it, but with probability $\exp (-\Delta E /T)$:

$$ \begin{equation} p(\text{flip}) = \begin{cases} 1 & \text{ if } \Delta E < 0\\ \mathrm{e}^{-\frac{1}{T} \Delta E} & \text{ otherwise.} \end{cases} \end{equation} $$

The Markov chain defined in this way satisfies the detailed balance condition and is ergodic. It thus converges to the true Boltzmann equilibrium distribution as we repeat the random spin flips ad infinitum.

The following Python code implements the algorithm. However, we implement a small trick that improves the running time. We note that the change in energy $\Delta E$ that we compute when flipping site $s_i$ depends only on $s_i$ and its neighbors. Nothing prevents us from updating also $s_j$ as long as $s_i$ and $s_j$ are not themselves neighbors. This means that we can update up to half of all the sites in a single step, instead of just one.

In practice the matrix $\small C = \begin{pmatrix} 0 & 1 & 0 \\ 1 & 0 & 1 \\ 0 & 1 & 0 \end{pmatrix}$ contains indices for the four neighbors of a given site. By performing a convolution (technically a cross-correlation) on the current state with the neighbors matrix, we find the sum of the neighboring spins which is then used to compute the change in the energy. To update half of the sites, we construct a binary matrix with a checkerboard pattern that will select the sites to update. On the next iteration we take the complement of that checkerboard pattern to select the other sites. We flip the spins according to the Metropolis probability defined above, but only for those sites where the checkerboard matrix is $1$. We repeat these steps for a selected number of times.

import numpy as np
from scipy.signal import correlate2d

def ising_model_metropolis_sample(n: int, T: float, num_iters: int):
    """
    Iterates the Ising model Metropolis dynamics for a fixed number
    of iterations. Returns a sample from the approximate equilibrium distribution.
    """
    j = 0
    C = np.array([[0, 1, 0], [1, 0, 1], [0, 1, 0]])
    s = np.ones((n, n))

    for _ in range(num_iters):
        j = 1 - j
        if j == 1:
            X = np.indices((n, n)).sum(axis=0) % 2
        else:
            X = 1 - np.indices((n, n)).sum(axis=0) % 2

        delta_E = 2 * s * correlate2d(s, C, mode='same', boundary='wrap')
        cond = np.where(np.logical_and(X == 1, delta_E < 0))
        s[cond] = -s[cond]
        probs = np.exp(-delta_E/T)
        U = np.random.rand(n, n)
        cond = np.where(np.logical_and(X == 1, np.logical_and(delta_E >=0, U < probs)))
        s[cond] = -s[cond]       
    return s

Not bad. This works pretty well, as long as $n$, the side of the square grid, is an even number. If it's not, the convolution boundary, which is wrapped around the edges, gets messed up, leading to some very interesting but wrong regular patterns (see figure 2).

Ising sample wrong — Figure 2: The convolution edge wrapping leads to erroneous regular patterns when the square grid has a side with odd length.

The sampling approach based on Metropolis dynamics works well but is approximate, because while we do converge to the equilibrium, we never really sample from it - we sample from its approximation. Sampling perfectly from the exact equilibrium is possible with a beautiful technique called Coupling from the past. However, the runtime for obtaining even a single sample becomes prohibitive even for very small $n$ when the temperature is below its critical point. Therefore, its main strength is to sample perfectly from the unmagnetized states when the temperature is supercritical.

Solving the Ising model

Solving the Ising model analytically roughly means obtaining expressions for the energy and magnetization as the temperature changes. Let's recall that the normalizing constant of the Boltzmann distribution is $Z = \sum_{S} \mathrm{e}^{-\beta E(S)}$. This quantity is very important in physics, where it's called the partition function.

The partition function is important because many quantities of interest can be expressed as a function of it. For example, the mean energy at equilibrium is given by $\mathbb{E}[E] = -\frac{\partial}{\partial \beta}\ln Z$, the variance by $\text{Var}(E) = \frac{\partial^2}{\partial \beta^2}\ln Z$, and the heat capacity by $\frac{\partial }{\partial T} \mathbb{E}[E]$. The quantity that appears most in these expressions is $\ln Z$ and typically we call $\lim_{n \rightarrow \infty} \frac{\ln Z}{n}$ the free energy per site of the system. The goal is, therefore, to calculate this quantity as all other interesting variables are just functions of it.

The partition function for a one-dimensional Ising chain is

$$Z = \sum_{\{s_i\}} \mathrm{e}^{-\beta E(S)} = \sum_{\{s_i\}} \mathrm{e}^{\beta \sum_ i s_i s_{i+1}} = \sum_{\{s_i\}} \prod_i \mathrm{e}^{\beta s_i s_{i+1}}. $$

We simply want to calculate this quantity. This can be done in an inductive manner. Let $Z_n$ be the partition function for a chain of size $n$ vertices. Then we separate $Z_n$ into two parts, representing the number of chains of length $n$ where the last site points up or down, respectively: $Z_n = Z_n^+ + Z_n^-$. Now, if we add a new site at the end, it can change the partition function in two ways. If its spin is the same as the spin of the last site, then the new edge has an energy of $-1$ and the contribution to $Z$ is a factor of $\mathrm{e}^{\beta}$. If the new vertex has a different spin than the last one, then it contributes a factor of $\mathrm{e}^{-\beta}$. We get the following relationships between $Z_n$ and $Z_{n+1}$:

$$\small \begin{pmatrix} Z_{n+1}^+ \\ Z_{n+1}^- \\ \end{pmatrix} = M \begin{pmatrix} Z_{n}^+ \\ Z_{n}^- \\ \end{pmatrix} \text{, where } M = \begin{pmatrix} \mathrm{e}^\beta & \mathrm{e}^{-\beta} \\ \mathrm{e}^{-\beta} & \mathrm{e}^\beta \\ \end{pmatrix} $$

The matrix $M$ describes how the partition function changes as $n$ increases. Importantly $n$ here is a spacial dimension, not a temporal one. The eigenvalues of $M$ are $\lambda_1 = \mathrm{e}^\beta + \mathrm{e}^{-\beta} = 2 \cosh \beta$ and $\lambda_2 = \mathrm{e}^\beta - \mathrm{e}^{-\beta} = 2 \sinh \beta$. As $n \rightarrow \infty$, $\lambda_1$ dominates and $Z$ grows as

$$ Z_n \sim \lambda_1^n = (2 \cosh \beta)^n $$

Then, the asymptotic free energy per site is

$$ f = \lim_{n \rightarrow \infty} \frac{\ln Z}{n} = \ln(2 \cosh \beta). $$

The expected energy per site is then

$$\mathbb{E}[E] = -\frac{1}{n} \frac{\partial}{\partial \beta} \ln Z = -\tanh \beta$$

and the variance of the energy per site is

$$ \text{Var}(E) = \frac{1}{n} \frac{\partial^2}{\partial \beta^2} \ln Z = 1 - \tanh^2 \beta. $$

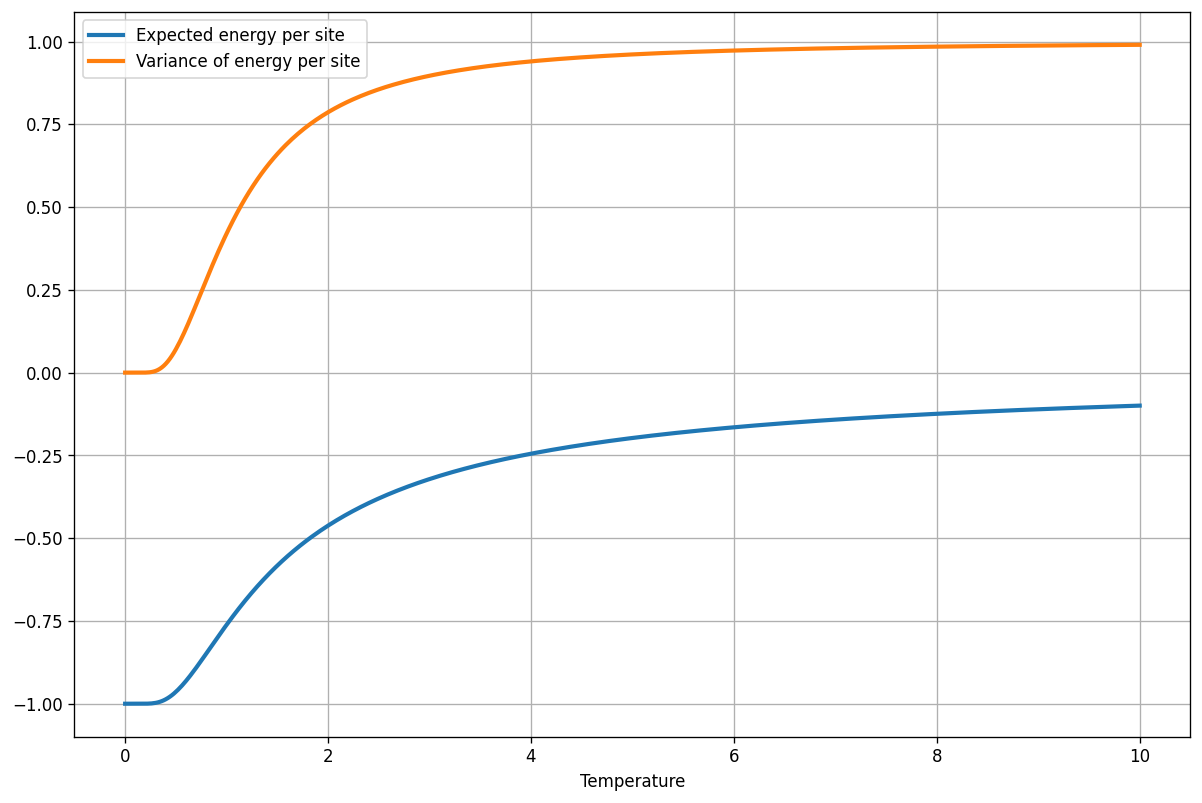
Ising equilibrium energy — Figure 3: The statistics of the equilibrium energy of the one-dimensional Ising model. As the temperature increases, the mean of the energy increases converging to 0, because the system becomes less magnetized. The variance also increases and converges to 1 as the states become equally probable.

Obtaining an exact solution for the two-dimensional case is possible, but complicated. Overall, I think the one-dimensional Ising model is quite useful because it yields a lot of intuition compared to the effort for solving it.