Phase Transitions in Computation | The Critical Section

One of my all-time favourite topics in theoretical computer science is that of phase transitions in computational problems. I think these are one of the most beautiful and incredible phenomena because of their mystic and fundamental nature. Unlike in physics, where phase transitions have been known for quite some time now, they are relatively new in computer science, where they first appeared in the 1990s. This post explores some very basic phase transitions in the 3-SAT problem. All content for this post comes from Cristopher Moore and Stephan Mertens' awe-inspiring book The Nature of Computation.

Phase transitions can be thought of as abrupt qualitative changes to the behaviour and characteristics of a system, dependant on specific values of key parameters in that system. Typical examples of phase transitions in physics are: - The transition of matter from a solid state to liquid state (melting) or from a liquid state to a solid state (freezing), - The emergence of superconductivity when cooling certain metals, - The phenomenon where some materials lose their permanent magnetic properties when heated above a certain temperature.

Here however, we'll be concerned with computational problems and our phase transitions will be interpreted as a rapid change in the amount of computation needed to find a solution to a given decision problem, or assert that none exists. Importantly, the problem instances will be random instead of the typical worst-case instances chosen by a malevolent adversary. This corresponds to evaluating the average case complexity - averaged across the different possible inputs.

Boolean satisfiability

The SAT problem is about satisfying boolean conditions. The input is a propositional logic formula in conjunctive normal form (CNF), defined on the boolean variables $x_1, x_2, ..., x_n$. I.e., the formula is expressed as a conjunction of many clauses (the conditions), each of which can be satisfied by either of the variables present inside it being true. The goal is to find an assignment of the variables $x_1, ..., x_n$ for which the formula is true. If each clause contains up to $k$ variables, we call this a $k$-SAT formula. For example, the formula

$$ \begin{align} \phi(x_1, x_2, x_3, x_4, x_5) =& \ (x_2 \vee \ \neg x_3 \vee \ \neg x_4) \ \wedge \\ & \ (x_1 \vee \ x_3 \vee \ x_5) \ \wedge \\ & \ (x_2 \vee \ x_3 \vee \ \neg x_1) \ \wedge \\ & \ (x_1 \vee \ x_3 \vee \ \neg x_2) \ \wedge \\ & \ (x_5 \vee \ \neg x_2 \vee \ \neg x_4) \ \wedge \\ & \ (x_1 \vee \ \neg x_2 \vee \ \neg x_5) \ \wedge \\ & \ (x_1 \vee \ x_5 \vee \ \neg x_3) \ \wedge \\ & \ (x_2 \vee \ x_3 \vee \ \neg x_4) \ \end{align} $$

takes in 5 variables, has 8 clauses and each clause can be satisfied by any of the three variables inside being true. Note that any variable can appear negated. We can verify that one solution is $x_1 = \text{true}$, $x_2 = \text{true}$, $x_4 = \text{false}$. The other two variables - $x_3$ and $x_5$ - are irrelevant and can be set to any boolean value.

Now that we know what the SAT problem is about, we can define a random formula by specifying a uniform distribution over 3-SAT formulas with $n$ variables and $m$ clauses. There are $M = 2^3 {n \choose 3}$ possible clauses because out of $n$ variables we need to choose 3, and each one of these can be negated. To generate a random formula we sample uniformly with replacement $m$ clauses out of the possible ones. The parameter governing the solvability of the sampled formula is the density of clauses to variables $\alpha = \frac{m}{n}$. We will see that this parameter directly controls the difficulty of any specific SAT instance.

For solving NP-complete problems like 3-SAT we can use a backtracking algorithm. Specifically, for 3-SAT we can use the DPLL algorithm (which stands for Davis, Putnam, Logemann, Loveland):

DPLL
  input: a SAT formula S
  output: is S satisfiable?
  begin
    if S is empty, return true;
    if S contains an empty clause, return false;
    select an unset variable x;
    if DPLL(S[x = true]) = true, return true;
    if DPLL(S[x = false]) = true, return true;
    return false;
  end

The algorithm operates as follows:

If the input formula contains no clauses, return trivially true;
If the input formula contains an empty clause, return false - this would be a trigger for example on the formula $(x_1 \vee x_2) \wedge () \wedge (\neg x_2)$;
Otherwise, select a variable and recursively check whether there is a solution when setting that variable to true or false. Setting a variable $x_i = \text{true}$ allows us to simplify the formula by deleting those clauses where that variable is encounted like $(... \vee x_i \vee ...)$ and remove the literals in those clauses where it's encountered like $(... \vee \neg x_i \vee ...)$. For example, if we set $x_2 = \text{true}$ in the formula $(x_1 \vee x_2) \wedge (x_3 \vee \neg x_2)$ we can simplify it to just $(x_3)$.

Selecting which variable to set, and to what value, can be done in different ways (some more efficient than others). One way is to:

set those variables that will satisfy any unit clauses
set those variables which are "pure" - only appear with one polarity
if there are no unit clauses or pure variables, choose a variable by prioritizing 2-clauses before 3-clauses.

The run-time cost of the DPLL algorithm is characterized mainly by the number of recursive calls that it has to make. In what follows, this will be the main metric for measuring the difficulty of SAT problem instances.

The Phase Transition

Let's call our distribution over random $k$-SAT formulas with $n$ variables and $m$ clauses $F_k(n, m)$. Then we can estimate the average probability of a formula from $F_k(n, m)$ being solvable by sampling a large number of formulas, solving each one of them with DPLL, and counting the number of instances where a solution exists. In particular we are interested how the probability of being solvable, as well as the number of function calls, depend on the clause-to-variable density $\alpha$.

The figure below shows how the probability of a random 3-SAT formula depends on $\alpha$ when $n=5$ and $n=30$. Two things are evident:

The higher $\alpha$ is, the less likely it is that the formula will be solvable. This is because with more clauses per variable, it becomes more likely that some of the clauses contain variables with opposite polarity which prevents the formula from being satisfied.
The more variables there are, the sharper is the decrease in the solvability as $\alpha$ increases. Formulas with $n=30$ variables become more rapidly unsolvable compared to formulas with $n=5$ variables. One can verify numerically that the corresponding graphs when $n=100$ or $n=200$ will be even steeper - for a large $n$ and up to some specific $\alpha_c$, the formulas will be solvable with high probability and above that $\alpha_c$ they will be unsolvable with high probability.

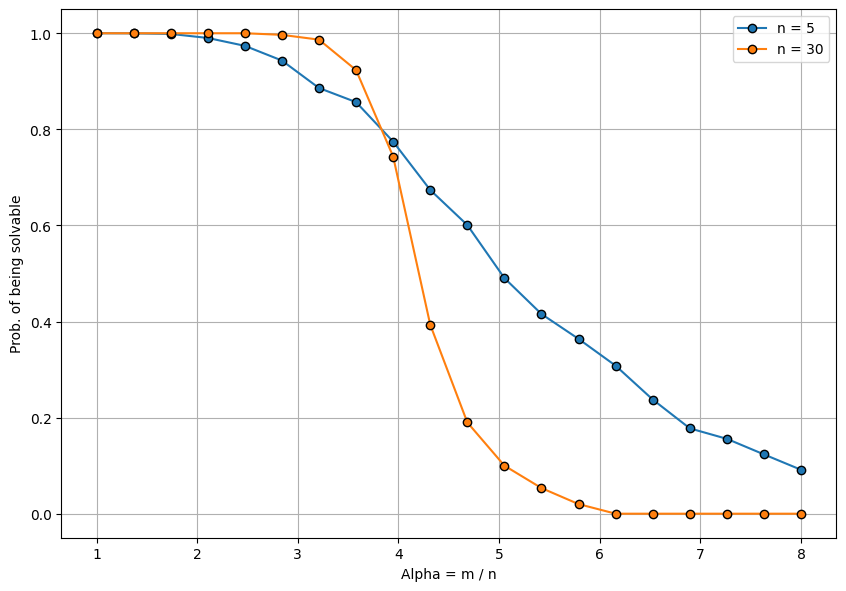
Probability of being solvable — Figure 1: The relationship between the clause-to-variable density and the probability of being solvable.

If we consider what happens when $n=\infty$, we expect to find one critical value of the clause-to-variable ratio $\alpha_c$ below which a formula is almost surely solvable while above it, it is almost surely unsolvable. This value $\alpha_c$ would be a critical point and the 3-SAT problem would undergo a qualitative change as it transitions from low to high $\alpha$.

More formally, the conjecture is that for each $k \ge 3$, there is a constant $\alpha_c$ such that

$$ \lim_{n \rightarrow \infty} P( F_k(n, m) \text{ is solvable}) = \begin{cases} 1 & \text{if } \alpha < \alpha_c(n) \\ 0 & \text{if } \alpha > \alpha_c(n) \end{cases} $$

Unfortunately, this conjecture still remains... a conjecture. The closest we've come to it is a theorem by Friedgut stating that for each $k \ge 3$, there is a function $\alpha_c(n)$ such that, for any $\epsilon > 0$,

$$ \lim_{n \rightarrow \infty} P( F_k(n, m) \text{ is solvable}) = \begin{cases} 1 & \text{if } \alpha < (1 - \epsilon) \alpha_c(n) \\ % & is your "\tab"-like command (it's a tab alignment character) 0 & \text{if } \alpha > (1 + \epsilon) \alpha_c(n). \end{cases} $$

This theorem is useful but fails to prove that $\alpha_c(n)$ converges to a constant as $n \rightarrow \infty$. Could it be that $\alpha_c(n)$ just keeps oscillating in some weird way, instead of converging? Wouldn't that be bizarre?

Deriving a lower bound on the critical point

It is hard to come up with rigorous bounds for $\alpha_c$. The best estimates right now state that $\alpha_c$ is between 3.52 and 4.49. To get a sense of the type of analysis done, in this section we'll prove one not particularly tight lower bound on $\alpha_c$.

Crucially, we rely on the following result:
Corollary: If for some constants $\alpha^*$ and $C > 0$

$$ \lim_{n \rightarrow \infty} P( F_k(n, m=\alpha^*n) \text{ is solvable}) \ge C, $$

then, for any constant $\alpha < \alpha^*$,

$$ \lim_{n \rightarrow \infty} P( F_k(n, m=\alpha n) \text{ is solvable}) = 1. $$

The above result means that when $n \rightarrow \infty$, if a random formula is satisfiable with positive probability at density $\alpha$, then formulas with lower density are satisfiable almost surely. Likewise, if the probability of a formula at a given density being solvable is bounded below 1, then this probability is zero at any higher density. This is a nice example of a zero-one law... Kolmogorov would be proud. In any case, this result implies that if we find such a $\alpha^*$ and assuming our phase transition conjecture is true, then $\alpha_c > \alpha^*$.

Before the actual analysis, it's useful to get a feel for how the runtime depends on the clause-to-variable density. The figure below shows how the number of DPLL calls scales as $\alpha$ increases.

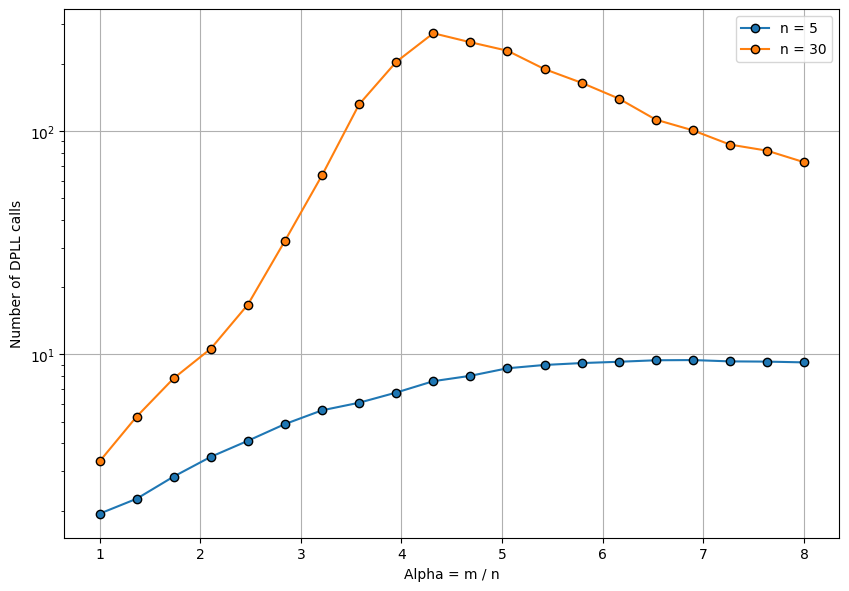
Importantly, for small $\alpha$, it is very easy to find a satisfying assignment because the clauses are few and most of the variables are not conflicting. The number of recursive calls is linear in the number of variables and the search process essentially comes down to evaluating a single branch of the resulting decision tree.

On the other extreme, for large $\alpha$ there are so many clauses per variable that many of them are conflicting each other and the formula is unsatisfiable. However, the more clauses there are, the earlier that contradictions appear in the search process - that is why the runtime eventually starts decreasing as $\alpha$ increases too much. With too many clauses, the contradictions are so many that the DPLL algorithm starts seeing unsatisfiable subproblems very learning in the search process, resulting in fewer recursive calls.

When $\alpha$ is around 4.3 (and $n=30$), the running time is maximal, because the number of clauses create enough variable conflicts so that DPLL has to do an exponential amount of backtracking. Contradictions appear not only often, but also at a bigger depth in the search process, compared to when $\alpha$ is large. Around this range is also the expected critical point $\alpha_c$, above which the formula becomes unsatisfiable with high probability.

Now, to derive the lower bound we model the unit clause (UC) variant of the DPLL algorithm with differential equations. The UC algorithm satisfies any unit clause first and if there are no unit clauses, chooses a random variable and sets it to true or false with equal probability. Most importantly, if it encounters any contradictions, it simply returns "Don't know" without backtracking. Thus, it is essentially evaluating a single decision branch in the tree formed by a proper backtracking algorithm. To define the state variables we choose $T$ to be the number of variables set to far and $n-T$ the number of unset ones. $S_1, S_2, S_3$ are the number of unit clauses, 2-clauses and 3-clauses, respectively.

The analysis relies on a specific type of conditional randomness. Suppose we start with a formula chosen uniformly at random and we set $T$ variables, producing a resulting formula with $S_1, S_2$, and $S_3$ clauses. Then, one can be convinced that this resulting formula is still uniformly random, but over those formulas with $n-T$ variables and with the same respective number of 1, 2, and 3-length clauses. The probabilities that we calculate next all rely on this fact.

A variable $x_i$ appears in a given 3-clause with probability $\frac{3}{n - T}$ (it's slightly larger if the variables in a clause have to be distinct, but this does not matter when $n \rightarrow \infty$). There are $S_3$ 3-clauses and therefore $x_i$ appears in $\frac{3 S_3}{n - T}$ clauses. This is also the rate at which 3-clauses disappear.

When we set $x_i$ to some boolean value, on average half of the 3-clauses in which $x_i$ appears disappear and half turn to 2-clauses. Therefore, $\frac{3 S_3}{2 (n - T)}$ 2-clauses appear on setting $x_i$. Similarly, the probability that $x_i$ belongs to a 2-clause is $\frac{2}{n - T}$ and 2-clauses disappear at the rate $\frac{2 S_2}{n - T}$.

Thus, we form a system of difference equations:

$$ \begin{align} \mathbb{E}[\Delta S_3] &= - \frac{3 S_3}{n - T} \\ \mathbb{E}[\Delta S_2] &= \frac{3 S_3}{2 (n - T)} - \frac{2 S_2}{n - T}. \\ \end{align} $$

When $n \rightarrow \infty$, these can be rescaled using $s_2 = \frac{S_2}{n}$, $s_3 = \frac{S_3}{n}$, and $t=\frac{T}{n}$, producing a system of differential equations:

$$ \begin{align} \frac{d s_3}{dt} &= - \frac{3 s_3}{1 - t} \\ \frac{d s_2}{dt} &= \frac{3 s_3}{2 (1 - t)} - \frac{2 s_2}{1 - t}. \\ \end{align} $$

The initial conditions are $S_3(0) = m$ and $S_2(0) = 0$ which after rescaling become $s_3(0) = \alpha$, and $s_2(0) = 0$. The solution to the system is

$$ \begin{align} s_3(t) &= \alpha (1 - t)^3 \\ s_2(t) &= \frac{3}{2} \alpha t (1 - t)^2. \\ \end{align} $$

The number of 2 and 3-clauses $S_2$ and $S_3$ scale as $\Theta(n)$ - at any point in the algorithm they scale linearly in the number of variables. However, their expected changes are $O(1)$ which makes them change relatively slow compared to their size. This makes them amenable to this differential equation approach. $S_1$, on the other hand, is $O(1)$ and changes as $O(1)$, which forces us to model it with a discrete branching process.

A variable $x_i$ appears on average in $\frac{2 S_2}{n - T}$ clauses and half of them will be turned into unit-clauses when setting $x_i$. Therefore the number of unit clauses we create at each step is

$$ \lambda = \frac{1}{2} \frac{2 S_2}{n - T} = \frac{s_2}{1 - t} = \frac{3}{2} \alpha t(1-t).$$

Now, the operation of the UC algorithm creates "cascades". If there are no unit clauses, suppose we randomly choose to set $x_i$. This creates $\lambda$ new unit clauses. On the next step we are forced to set a variable that will satisfy any of these unit clauses. This, however, still creates $\lambda$ unit clauses on average, and so on. The expected number of steps needed to satisfy all the eventual resulting unit clauses, including the first step that set the cascade off, is

$$ 1 + \lambda + \lambda^2 + \lambda^3 + ... $$

If $\lambda > 1$, then the unit-clauses proliferate exponentially and as soon as we enounter a contradiction where two of them demand different values for the same variable, UC fails. This occurs with constant probability when the number of unit clauses reaches $\Theta(\sqrt{n})$ (due to the birthday paradox).

If $\lambda < 1$, the total number of unit clauses converges to $\frac{1}{1 - \lambda}$. The UC algorithm manages to satisfy all unit clauses, after which it again gets to select a random variable and set it to a random value. Thus, for UC to succeed on average, we need $\lambda < 1$. After maximizing over $t$, $\frac{3}{2} \alpha t(1-t)$ is less than 1 if $\alpha < \frac{8}{3}$. The probability that UC fails when the branching process is subcritical is still a positive constant, because the probability that two unit clauses contradict each other is $\Theta(\frac{1}{n})$ and there are $\Theta(n)$ steps in the algorithm. However, the positive probability of succeeding is enough to use the above corolary to say that the formula is satisfiable with high probability when $\alpha < \frac{8}{3}$. In these cases there is also positive probability that a proper DPLL algorithm finds a solution with no backtracking, which becomes exponentially difficult when $\alpha > \frac{8}{3}$.

To recap, when $\alpha < \frac{8}{3}$, the probability of UC failing is $O(1)$ - bounded from above - which means that the probability of UC succeeding is positive. The corollary stated above then implies that

$$ \lim_{n \rightarrow \infty} P( F_k(n, m=\alpha n) \text{ is solvable}) = 1, \ \forall \alpha < \frac{8}{3}. $$

And therefore $\alpha_c \ge \frac{8}{3}$. More sophisticated variants of DPLL yield better bounds, closer to the presumably true critical point value of approximately $4.267$. These constructive proofs fail, though, when backtracking becomes necessary. Other bounds can be obtained using non-constructive proofs which are a different approach altogether.