Deep Learning at Scale
As the scale of my ML projects started to increase, I have found myself in need of understanding more and more the actual engineering aspects around the models. I am perfectly fine with deep learning being an engineering-first discipline, rather than a theory-first one. Yet there are considerably more high-quality sources about the algorithms than about the implementation tricks needed. This post attempts to summarize important knowledge useful in understanding how to scale the modern deep learning approach to larger datasets, more nodes, and across different accelerators. Most likely, this is the first of multiple such posts.
Implementation
To start, I think it pays to understand what happens when a forward pass is executed. And for that, let's explore a bit how PyTorch works under the hood. Ultimately, calculating the outputs of a neural network natively in Python will be too slow, due to the interpreter wasting too much time decoding every single line. Thus, it is natural that at some lower level the critical computations be executed in a faster language. Consider the forward pass of the nn.Conv2d module from PyTorch. Here's what happens:
- The source code of
nn.Conv2dis actually a thin wrapper storing the weights, bias, and any other parameters. For the actual forward pass,F.conv2dis called. - Now my Python debugger starts skipping this call when I try to step into it, indicating that
F.conv2dis a binary file. Nonetheless, we can find the source code, currently atpytorch/aten/src/ATen/native/Convolution.cpp. Looking at the commit taggedv2.0.0, the functionconv2dtakes in various parameters like input, weight, bias, stride, padding, and dilation, performs some basic checks, and callsat::convolution. - In turn,
at::convolutionreads a global context, specifically whether the underlying CuDNN module should be in deterministic mode. It then callsat::_convolution. - This function extracts all the convolution arguments into a small container and checks whether all weights and biases are consistent with the input size. Next, it selects a backend - one of the libraries optimized for the specific hardware that is available at execution time - e.g. Nvidia GPUs offer a specific library, CuDNN, for highly optimized neural net calculations. Alternative backends available are CPU (including whether to use various advanced features like AVX), CUDA, OpenMP, MKL. It is a great design choice to allow higher-level functions be agnostic to the underlying low-level calculations.
- Let's suppose that CuDNN has been selected as a backend. Then the subsequent function is
at::cudnn_convolutionwhich itself callsat::cudnn_convolution_forward. The latter checks whether all inputs and weights are on the same GPU and callsraw_cudnn_convolution_forward_out. This is where it gets particularly interesting. Here, depending on the precision we may callraw_cudnn_convolution_forward_out_32bitwhich itself, finally, calls thecudnnConvolutionForwardlibrary function. Ultimately, CuDNN is a closed-source library and we can't inspect any deeper than this. But we can actually choose which convolution algorithm to use from either an implicit general matrix-matrix algorithm (GEMM) or a transform-based algorithm such as FFT or Winograd. If the proper flag is enabled, the library can run different algorithms to benchmark their performance and choose the best one for future use on similarly sized inputs. Alternatively, an algorithm can be chosen based on heuristics. After that, we get the convolution output.
A similar design is used with all other modules, for both forward and backward calls. For example, the considerably simpler F.grid_sample calls at::grid_sampler, which calls cudnn_grid_sampler, which calls the CuDNN function cudnnSpatialTfSamplerForward. Likewise, for the backward there is cudnnSpatialTfSamplerBackward.
Hence, one can see that executing even a simple module requires traversing a deep call stack, the necessity of which comes from the requirement to support multiple backends, each optimized for a different hardware configuration. Moreover, some of the fastest algorithms are non-deterministic and may produce slightly different results compared to the deterministic variants. Libraries like CuDNN offer the possibilities to use only deterministic algorithms with/or without benchmarking for selecting the best one. I find it fascinating how much analysis can go in trying to squeeze out as much performance as possible from these low-level components.
Distributed Training
Larger datasets may require more than one GPU in order to train the model in a reasonable amount of time. The most common approach is by parallelizing the dataset samples across the GPUs and it falls in the SPMD category - single program multiple data. PyTorch offers a few different ways to achieve this.
The first one is torch.nn.DataParallel (DP). When initialized, this module wraps the model, retrieves the indices of all available GPUs, whose number let's say is \(G\), sets the output device and performs various checks. When the forward is called the input tensor is chunked along the batch dimension into \(G\) parts of approximately the same size. The \(i\)-th chunk is sent to the \(i\)-th GPU in a process called scattering. Subsequently, the model is also replicated to those GPUs. This requires, in simple terms, the copying of the module's children (submodules), parameters and buffers (non-trainable parameters like the running mean and standard deviation for BatchNorms). The process is called broadcasting because a single object, the module, is sent to all participating devices. Subsequently, the model is called on all of them. This happens by literally creating a bunch of threading.Threads in the context of which each model replica is ran. Finally, the predictions are gathered from all devices and concatenated.
In the backward pass, gradients flow back through the individual devices, after which they are gathered on the primary device and then summed/averaged. Overall, in this approach there is one process in which we replicate the model to all GPUs in every single forward pass. This does not take much time, since the GPUs belong to the same host. For the parallel forward pass, in principle Python’s GIL can be a limiting factor for CPU-bound parallel tasks because it allows only one thread to execute Python bytecode at a time. However, for I/O-bound tasks or tasks that primarily involve executing compiled code (like PyTorch operations on GPUs), this is less of an issue.
PyTorch offers also torch.nn.parallel.DistributedDataPrallel (DDP) which is a significant generalization. Here instead of a single process, we will have one process per GPU, all the processes will form a process group, and they will synchronize the gradients via actual inter-process communication (IPC). This also allows training on multiple nodes and avoids any GIL contention.
The overall idea is that multiple processes run on multiple GPUs separately. Each process computes the forward pass only on a portion of the whole dataset. After the gradients are calculated, they are broadcasted to all other processes where they are averaged in a process called AllReduce, and applied to each model replica. This happens at every training iteration and prevents any divergence in the model parameters across the devices.
Broadcasting the local gradients to the other devices in a naive way is very slow, because this would require calling AllReduce on every single parameter tensor, many of which are of small size. It is much more efficient and fast to batch multiple tensors into larger buckets and AllReduce the buckets directly. Thus, when initializing the DDP wrapper, the module is replicated to all devices and subsequently each parameter is assigned to one bucket. The buckets are ordered and the parameters closer to the last layer are put in the first few buckets, while those from the first layer are put in the last few buckets. It is important that bucket \(i\) on device \(p\) contains exactly the same parameters as bucket \(i\) on device \(q\).
The number of buckets can have a noticeable effect on performance. In principle, using as many buckets as parameter tensors defeats the purpose of using buckets in the first place. On the other hand, using a single bucket requires waiting for the backward pass to completely finish before launching the AllReduce. With any number of buckets in between, one can overlap the gradient computations with the asynchronous communications.
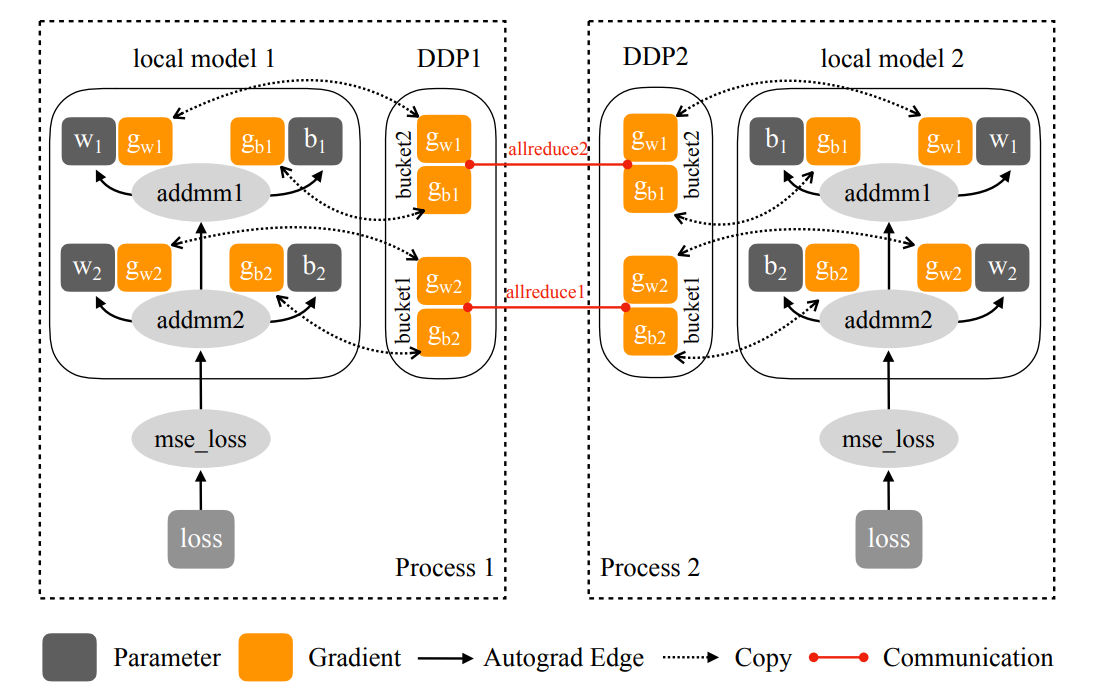
Gradients are populated from the last layer backwards. Hence, we can launch the AllReduce for one bucket as soon as all the gradients for those tensors which belong to it are computed, saving a lot of time in the process. In practice, DDP registers an autograd hook for each parameter tensor which is activated after the gradients for that tensor are computed. Within the hook the appropriate offset in the bucket is found and the gradients are copied in their location. Then, if all gradients in the bucket have been computed, the bucket is marked ready. Then, AllReduce is launched on all ready buckets in order. Finally, the reduction is wait-ed and the averaged gradients are written over the current gradients computed over the local replica's data batch.
There are some complications however. Consider that Torch supports dynamic computation graphs and suppose a model uses an if branch to select one of two possible layers to use for the forward pass. Naturally, only gradients for one of the layers will be computed. As a result, the buckets to which belong the parameters of the layer that was not used will never be marked ready... and training will hang. For that reason DDP offers the argument find_unused_parameters which will scan the parameters, find those which are not used and mark them as ready, so they don't hinder the communication.
It is also interesting how the AllReduce computation works. Suppose we have \(N\) processes, each on a separate GPU device. Each device \(i\) also holds \(M\) gradients \( g_1^i, ..., g_M^i\). Assuming the reduction operation is addition, the goal is to compute the reduced gradients $ \sum_{i=1}^N g_1^i, ..., \sum_{i=1}^N g_M^i $ and to distribute them to all nodes.
In reality, the topology of how the nodes are connected informs the algorithm to use. Or better said, each possible algorithm relies on an assumption of how the devices are logically connected. In a star topology all gradients may be sent to one particular node which then reduces them and distributes the result back. This is simple and fast, but it does not scale well due to communication bottlenecks in the main device. A tree topology offers better scalability but may have uneven bandwidth. Instead, the ring has become a good choice, offering increased bandwidth efficiency at the cost of slightly higher latency.
In a ring-based all-reduce the devices form a ring, each one communicating only with its neighbors on the left and right. We proceed as follows. Device \(i\) cuts its gradients into \(N\) parts, which we call \(\mathbf{b}_1^i, ..., \mathbf{b}_N^i\). It sends \(\mathbf{b}_i^i\) to its neighbor on the right and similarly receives \(\mathbf{b}\_{i-1}^{i-1}\) from its left neighbor. At the next step, device \(i\) reduces the received gradients with its own corresponding chunk \(\mathbf{b}\_{i-1}^i\) and sends the result \(\mathbf{b}\_{i-1}^{i-1} + \mathbf{b}\_{i-1}^i\) to the right neighbor, while receiving a reduced chunk from its left neighbor. This process continues for \(N-1\) steps until each device has one chunk which is fully reduced. Then, all that remains is for each device to distribute that chunk to the others. This takes \(N-1\) additional steps after which the AllReduce has been completed.

The ring-based approach is usually hidden from the end-user. One typically uses a library that already implements and optimizes all the collective communications between the devices. For example, NVidia offers NCCL which provides a convenient function ncclAllReduce that dynamically chooses which algorithm to use depending on the available hardware. Upon initialization, NCCL gathers information about the GPUs - how they are connected (e.g. PCIe or NVLink) and what are their bandwidth characteristics. Based on this, it determines which algorithm to select for the AllReduce. Moreover, the individual GPU-to-GPU data transfers are very quick, since they can avoid copying the data into main memory.
While NCCL may be the most efficient and fast library for NVidia GPUs, it is certainly not the most popular. The Message Passing Interface (MPI) has been the de-facto standard for parallel computing for decades. Most other major libraries are built on its concepts of size, rank, local rank, and the collective communication functions like AllReduce, AllToAll, and AllGather.
The idea is quite simple. Suppose we run a training job on 6 nodes, each with 8 GPUs. Then the total world size is 48, and the local size within each node is 8. Each GPU will be identified by its local rank from 0 to 7 within the node, and at the same time with its global rank from 0 to 47. All the common functions for point-to-point communication like send, recv, isend, irecv identify the devices by their ranks.
The torch.distributed package manages quite well to abstract away all the complexity related to the communication libraries. Like before, it refers to them as different backends which the user selects and sets the environment for. However, to coordinate the overall distributed training process, a higher-level communication package called c10d is used. It takes care of the overall training process.
In general, the script is started on all devices either manually by spawning all the processes or automatically by using a launcher like torchrun. After the processes (workers) are initialized, they need to find each other. Thus, c10d requires that the user set a master IP address and port (belonging to one of the nodes) where all the workers will rendezvous. Once they connect to the master address, they can identify each other, establish a process group, synchronize initially, and then begin training.
Since each worker will be training on a subset of the dataset, one needs to use a DistributedSampler in the dataloader. With \(N\) GPUs, and a batch size of \(B\), the effective batch size per update will be \(NB\). Hence, a total of \(N\) times fewer updates will be performed. It is also common to increase the learning rate \(N\) times to keep the total distance travelled in weight space roughly the same.
Overall, this covers the basic elements of distributed training. There are many other interesting details I didn't cover, for example how to optimize the data loading process or how to debug and profile these systems. Additionally, the distributed training discussed here is entirely synchronous. Alternative approaches based on asynchronous parameter servers such as those in federated learning or in some reinforcement learning agents are also a big topic. In those settings there are other interesting problems such as gradients from one worker becoming stale before they are applied on the main server. But I'll leave these for a future post.